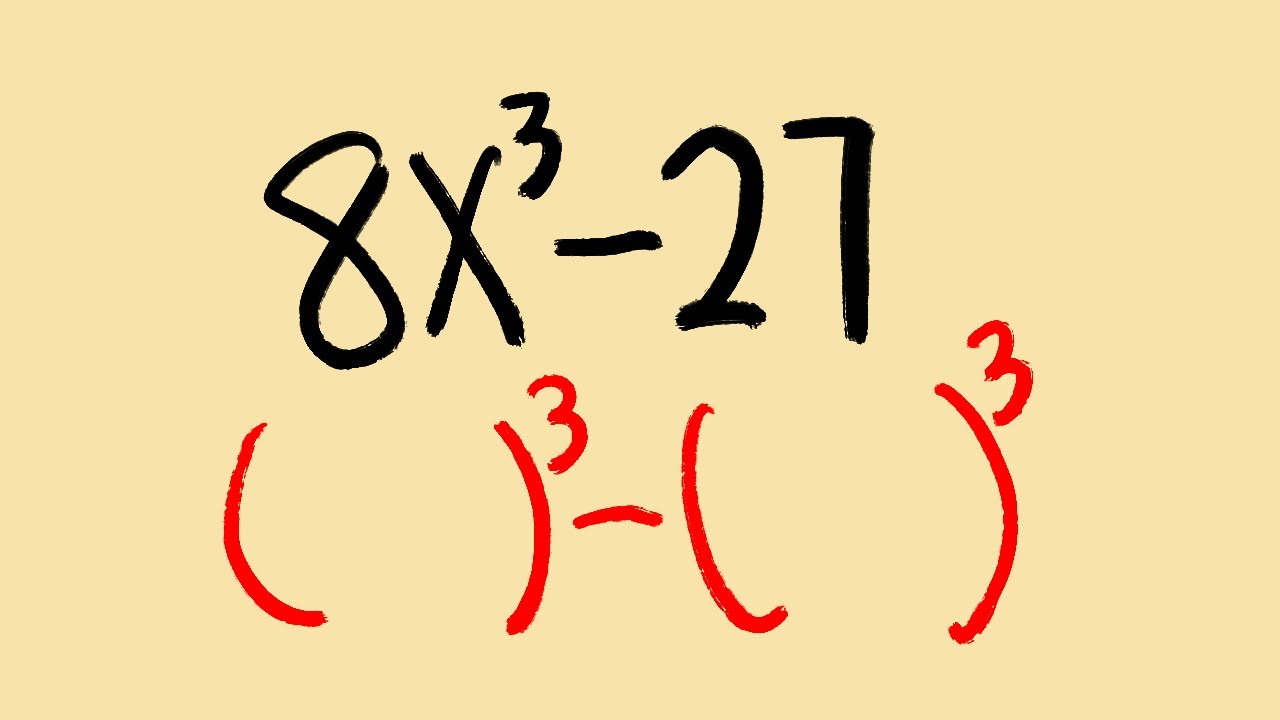Optimized Guide To Factor 8x 3 125: From Basics To Advanced Insights

The expression "factor 8x 3 125" is an intriguing numerical challenge that combines several mathematical concepts. It encompasses multiplication, exponentiation, and factoring, offering a holistic view of how numbers interact within mathematical frameworks. By dissecting each part, we aim to provide clarity and insight into the processes that govern this expression. With a structured approach, we'll break down each element, shedding light on the roles they play and the outcomes they produce.

For learners and enthusiasts alike, delving into the world of numbers can be both exciting and enlightening. This article is crafted to cater to a wide audience, ensuring that both novices and seasoned mathematicians find value in our exploration. By the end of this comprehensive guide, you'll have a clearer understanding of "factor 8x 3 125" and how it fits into the broader landscape of mathematical expressions.

Table of Contents

• The Basics of Multiplication: Breaking Down 8x 3 125
• What Does 'Factor' Mean in Mathematics?
• How to Factorize Numbers: A Step-by-Step Guide
• Exploring Multiples and Factors of 8, 3, and 125
• Why is Factorization Important?
• The Role of Exponents in Factor 8x 3 125
• Common Mistakes When Factoring: How to Avoid Them?
• How Does Factorization Apply in Real-World Scenarios?
• Advanced Techniques in Factoring
• The Connection Between Factorization and Algebra
• Historical Significance of Factoring in Mathematics
• How to Practice Factorization Effectively?
• FAQs on Factor 8x 3 125
• Conclusion

The Basics of Multiplication: Breaking Down 8x 3 125

To grasp the essence of "factor 8x 3 125," it's essential to first understand the multiplication process inherent in this expression. Multiplication is a fundamental mathematical operation that involves combining groups of equal size. In this case, the expression can be dissected into its components: 8, 3, and 125.

Each number in the expression plays a critical role. The number 8 can be seen as a collection of eight units, while 3 represents three such groups, and 125 is the multiplicand that these numbers will interact with. By multiplying these numbers, we can determine the total sum or product, which is a vital step in understanding the larger picture.

Breaking it down further:

• 8: This is the first factor, representing a group of eight units or items.
• 3: This factor signifies three groups of the initial set of units.
• 125: The final number in the equation, representing the multiplicand that is to be factored.

By multiplying these numbers, we find the product, which serves as the foundation for further analysis and factorization.

What Does 'Factor' Mean in Mathematics?

In mathematics, "factor" refers to a number or algebraic expression that divides another number or expression evenly, without leaving a remainder. It is a fundamental concept in arithmetic and algebra, used to simplify equations, solve problems, and understand number theory.

To factor a number means to break it down into its simplest components, known as factors or divisors. This process is crucial for various mathematical applications, as it allows for a deeper understanding of how numbers interact and relate to one another.

Factors are the building blocks of numbers, and their identification is a critical step in many mathematical processes. By understanding the concept of factors, one can gain insights into the structure and properties of numbers, enabling more efficient problem-solving and analysis.

How to Factorize Numbers: A Step-by-Step Guide

Factorizing numbers involves breaking them down into their prime components. This process can be achieved through a series of steps, each aimed at simplifying the number into its basic elements. By following these steps, one can effectively factorize numbers and understand their underlying structure.

Step 1: Identify the Number

The first step in factorizing a number is to identify the number you wish to factorize. In this case, we are focusing on the number 125, which is a component of the expression "factor 8x 3 125."

Step 2: Find the Prime Factors

Prime factors are numbers that are only divisible by 1 and themselves. To factorize a number, you must identify its prime factors, which serve as the building blocks of the number.

• Divide the number by the smallest prime number (2) and continue dividing until it is no longer divisible.
• Move to the next smallest prime number (3) and repeat the process.
• Continue this process with successive prime numbers (5, 7, 11, etc.) until the number is fully factorized.

Step 3: Express the Number as a Product of Prime Factors

Once you have identified the prime factors, express the number as a product of these factors. For example, the number 125 can be factorized as 5 x 5 x 5, or 5³.

Step 4: Verify the Factorization

After factorizing the number, verify the factorization by multiplying the prime factors together to ensure they equal the original number.

By following these steps, you can effectively factorize numbers and gain insights into their structure and properties.

Exploring Multiples and Factors of 8, 3, and 125

The numbers 8, 3, and 125 are integral components of the expression "factor 8x 3 125." Each of these numbers has its own set of multiples and factors, which are essential for understanding the expression's structure and implications.

Let's explore these numbers in more detail:

Multiples and Factors of 8

• Multiples: The multiples of 8 are obtained by multiplying 8 by whole numbers. Examples include 8, 16, 24, 32, 40, 48, etc.
• Factors: The factors of 8 are numbers that divide 8 evenly without leaving a remainder. These include 1, 2, 4, and 8.

Multiples and Factors of 3

• Multiples: The multiples of 3 are obtained by multiplying 3 by whole numbers. Examples include 3, 6, 9, 12, 15, 18, etc.
• Factors: The factors of 3 are numbers that divide 3 evenly without leaving a remainder. These include 1 and 3.

Multiples and Factors of 125

• Multiples: The multiples of 125 are obtained by multiplying 125 by whole numbers. Examples include 125, 250, 375, 500, 625, 750, etc.
• Factors: The factors of 125 are numbers that divide 125 evenly without leaving a remainder. These include 1, 5, 25, and 125.

By understanding the multiples and factors of these numbers, we gain insights into their relationships and interactions within the expression "factor 8x 3 125."

Why is Factorization Important?

Factorization plays a crucial role in mathematics, serving as a foundational concept for problem-solving and analysis. Understanding the importance of factorization helps us appreciate its applications and significance in various mathematical contexts.

The benefits of factorization include:

• Simplification: Factorization simplifies complex expressions, making them easier to understand and analyze. By breaking down numbers into their prime factors, we can identify patterns and relationships that are not immediately apparent.
• Problem Solving: Factorization is a valuable tool for solving equations and mathematical problems. By identifying the factors of a number, we can determine its divisors, identify common factors, and solve equations more efficiently.
• Number Theory: Factorization is a fundamental concept in number theory, providing insights into the properties and relationships of numbers. By understanding the factors of a number, we can gain a deeper understanding of its structure and behavior.
• Applications: Factorization has numerous applications in real-world scenarios, including cryptography, data encryption, and computer algorithms. By understanding the factors of a number, we can develop more efficient and secure systems for processing and transmitting data.

Factorization is an essential concept in mathematics, providing insights and tools for problem-solving, analysis, and applications in various contexts.

The Role of Exponents in Factor 8x 3 125

Exponents play a significant role in the expression "factor 8x 3 125," providing a concise and efficient way to represent repeated multiplication. Understanding the role of exponents is crucial for comprehending the structure and implications of this expression.

In mathematics, an exponent is a number that indicates how many times a base number is multiplied by itself. Exponents are used to express large numbers in a more compact form, simplifying calculations and analysis.

In the expression "factor 8x 3 125," exponents are used to express the prime factorization of the number 125. The number 125 can be factorized as 5 x 5 x 5, or 5³, using an exponent to represent the repeated multiplication of the base number 5.

Exponents are a powerful tool in mathematics, providing a concise and efficient way to express and analyze complex expressions. By understanding the role of exponents in the expression "factor 8x 3 125," we can gain insights into its structure and implications.

Common Mistakes When Factoring: How to Avoid Them?

Factoring can be a challenging process, and common mistakes can lead to incorrect results and misunderstandings. By understanding these mistakes and how to avoid them, we can improve our factoring skills and ensure accurate results.

Mistake 1: Misidentifying Prime Factors

One common mistake when factoring is misidentifying the prime factors of a number. This can occur when dividing the number by non-prime numbers or failing to consider all possible prime factors.

To avoid this mistake, ensure that you only divide the number by prime numbers and consider all possible prime factors. Use a prime factorization chart or calculator to verify your results and ensure accuracy.

Mistake 2: Skipping Steps

Another common mistake is skipping steps in the factoring process, leading to incomplete or inaccurate results. This can occur when trying to simplify the process or when assuming that certain steps are unnecessary.

To avoid this mistake, follow a step-by-step approach to factoring, ensuring that you complete each step thoroughly and accurately. Double-check your work and verify your results to ensure accuracy.

Mistake 3: Incorrectly Applying Exponents

In some cases, incorrect application of exponents can lead to errors in factorization. This can occur when misinterpreting the meaning of an exponent or failing to apply it correctly in calculations.

To avoid this mistake, ensure that you understand the meaning of exponents and how they are applied in calculations. Use a calculator or double-check your work to verify your results and ensure accuracy.

By understanding and avoiding these common mistakes, we can improve our factoring skills and ensure accurate results in mathematical analysis and problem-solving.

How Does Factorization Apply in Real-World Scenarios?

Factorization is not just a theoretical concept; it has numerous practical applications in real-world scenarios. Understanding how factorization applies in various contexts helps us appreciate its significance and value in everyday life.

Some real-world applications of factorization include:

• Cryptography: Factorization plays a crucial role in cryptography and data encryption, providing a secure and efficient way to encode and decode information. By understanding the factors of a number, we can develop secure algorithms for transmitting and processing data.
• Computer Algorithms: Factorization is used in computer algorithms to optimize calculations and improve efficiency. By breaking down numbers into their factors, we can develop more efficient algorithms for solving complex problems and analyzing data.
• Engineering: Factorization is used in engineering to simplify complex calculations and analyze structures. By understanding the factors of a number, we can determine the properties and behavior of materials and systems.
• Finance: Factorization is used in finance to analyze and predict market trends and behavior. By understanding the factors of a number, we can develop more accurate models for predicting and analyzing financial data.

Factorization is a valuable tool in various real-world scenarios, providing insights and solutions for a wide range of applications and contexts.

Advanced Techniques in Factoring

Factoring is a fundamental concept in mathematics, but it also involves advanced techniques that can enhance our understanding and analysis of complex expressions. By exploring these techniques, we can gain deeper insights into the structure and properties of numbers.

Technique 1: Polynomial Factoring

Polynomial factoring is an advanced technique used to simplify complex polynomial expressions. By breaking down a polynomial into its factors, we can identify patterns and relationships that are not immediately apparent.

To factor a polynomial, we can use techniques such as grouping, the distributive property, and the quadratic formula to identify its factors and simplify the expression.

Technique 2: Factoring by Substitution

Factoring by substitution is an advanced technique used to simplify complex expressions by replacing variables with known values. By substituting variables with their corresponding values, we can identify patterns and relationships that are not immediately apparent.

This technique is particularly useful for solving equations and simplifying expressions in algebra and calculus.

Technique 3: Factoring with Complex Numbers

Factoring with complex numbers is an advanced technique used to simplify expressions involving complex numbers. By breaking down complex numbers into their factors, we can identify patterns and relationships that are not immediately apparent.

This technique is particularly useful for solving equations and simplifying expressions in advanced mathematics and physics.

By exploring and applying these advanced techniques, we can enhance our understanding and analysis of complex expressions and gain deeper insights into the structure and properties of numbers.

The Connection Between Factorization and Algebra

Factorization and algebra are closely connected concepts in mathematics, providing a foundation for problem-solving and analysis. Understanding the relationship between these concepts helps us appreciate their significance and value in mathematical analysis.

In algebra, factorization is used to simplify expressions and solve equations. By breaking down expressions into their factors, we can identify patterns and relationships that are not immediately apparent, enabling more efficient problem-solving and analysis.

Factorization is also used in algebra to identify common factors and solve equations more efficiently. By understanding the factors of a number, we can determine its divisors and identify common factors, enabling more accurate and efficient solutions.

The connection between factorization and algebra is a fundamental concept in mathematics, providing insights and tools for problem-solving and analysis in various contexts.

Historical Significance of Factoring in Mathematics

Factoring has a long and rich history in mathematics, playing a crucial role in the development of mathematical concepts and theories. Understanding the historical significance of factoring helps us appreciate its value and contributions to the field of mathematics.

Factoring has been used for centuries to simplify complex expressions and solve mathematical problems. Ancient mathematicians, such as the Greeks and Egyptians, used factoring to solve equations and develop mathematical theories.

In more recent history, factoring has played a significant role in the development of modern mathematics and computer science. It has been used to develop algorithms and models for solving complex problems and analyzing data, contributing to advancements in fields such as cryptography and data encryption.

The historical significance of factoring in mathematics is a testament to its value and contributions to the field, providing insights and solutions for a wide range of applications and contexts.

How to Practice Factorization Effectively?

Practicing factorization effectively is crucial for developing and improving our factoring skills and understanding. By following these tips and techniques, we can enhance our understanding and analysis of complex expressions and gain deeper insights into the structure and properties of numbers.

Tip 1: Use a Step-by-Step Approach

Using a step-by-step approach to factorization is essential for ensuring accuracy and understanding. By following a series of steps, we can break down complex expressions into their factors and identify patterns and relationships that are not immediately apparent.

Tip 2: Practice with Real-World Examples

Practicing with real-world examples is a valuable way to enhance our understanding and analysis of factorization. By applying factorization techniques to real-world scenarios, we can gain insights into its applications and significance in everyday life.

Tip 3: Use Online Resources and Tools

Using online resources and tools is a valuable way to enhance our understanding and practice of factorization. Online calculators, tutorials, and practice problems can provide valuable insights and solutions for improving our factoring skills and understanding.

By following these tips and techniques, we can practice factorization effectively and enhance our understanding and analysis of complex expressions and mathematical concepts.

FAQs on Factor 8x 3 125

Here are some frequently asked questions about the expression "factor 8x 3 125" and their answers:

• What is the product of 8x 3 125? The product of 8x 3 125 is 3,000.
• What are the prime factors of 125? The prime factors of 125 are 5, 5, and 5, or 5³.
• How can I factor the expression 8x 3 125? To factor the expression 8x 3 125, break it down into its prime factors: 2 x 2 x 2 x 3 x 5 x 5 x 5.
• Why is factorization important in mathematics? Factorization is important in mathematics because it simplifies complex expressions, aids in problem-solving, and provides insights into the structure and properties of numbers.
• What are some common mistakes when factoring? Common mistakes when factoring include misidentifying prime factors, skipping steps, and incorrectly applying exponents.
• How can I practice factorization effectively? To practice factorization effectively, use a step-by-step approach, practice with real-world examples, and use online resources and tools.

Conclusion

The expression "factor 8x 3 125" is a fascinating mathematical challenge that combines several fundamental concepts, including multiplication, factorization, and exponents. By breaking down each component and exploring its implications, we gain insights into the structure and properties of numbers, enabling more efficient problem-solving and analysis.

Understanding the intricacies of factorization is crucial for mathematical analysis and problem-solving, providing valuable tools and insights for a wide range of applications and contexts. By practicing factorization effectively and exploring its real-world applications, we can enhance our understanding and appreciation of this essential mathematical concept.

With a deeper understanding of "factor 8x 3 125," we can approach mathematical challenges with confidence and clarity, unlocking new insights and solutions for a wide range of problems and scenarios.